The apparent magnitude of a celestial object, such as a star or galaxy, is the brightness measured by an observer at a specific distance from the object. The smaller the distance between the observer and object, the greater the apparent brightness.

(left) Two stars, A and B, with the same apparent magnitude. (right) However, star A is actually a more luminous star that is further away from the Earth than than star B.

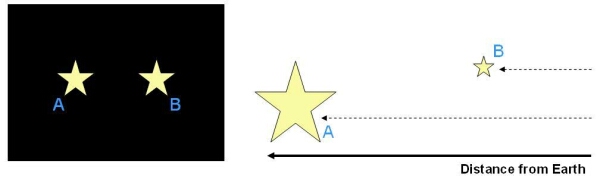
Two objects that have the same apparent magnitude, as seen from the Earth, may either be:

• At the same distance from the Earth, with the same luminosity.
• At different distances from the Earth, with different values of luminosity (a less luminous object that is very close to the Earth may appear to be as bright as a very luminous object that is a long distance away).

To convert the apparent magnitude, m, of a star into a real magnitude for the star (absolute magnitude, M), we need to know the distance, d to the star. Alternatively, if we know the distance and the absolute magnitude of a star, we can calculate its apparent magnitude. Both calculations are made using:

with m - M known as the distance modulus and d measured in parsecs.

The apparent magnitudes, absolute magnitudes and distances for selected stars are listed below:

Although Rigel and Deneb have the same real brightness (the same absolute magnitude), Rigel appears brighter than Deneb on the sky (it has a smaller apparent magnitude) because it is much closer to the Earth.