SAO Maths Primer

Mathematics Primer: Differential Equations

A differential equation is an equation that consists of an unknown function and its derivatives.

Suppose a quantity x changes at a rate that at any instant of time t is proportional to the amount x present at that instant. This can be expressed by the differential equation:

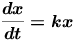
where k is a proportionality constant. The initial condition x=x₀ when t=0 enables us to evaluate the constant k .

As an example we display the equation of radiative transport (which those of you studying the advanced SAO Unit HET611 Intoduction to Stellar Astrophysics will find in from Module 6 "Stellar Interiors", Activity 2 "Energy Transport").

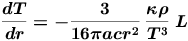This equation shows how the rate of change of temperature T , with radius r , is related to several quantities describing the stellar interior and is inversely proportinal to the cube of the temperature itself.

See also: derivative

Recommended Web Sites:

Eric Weisstein's world of Mathematics mathworld.wolfram.com

S.O.S. Mathematics www.sosmath.com

Return to Maths Primer page

Back to the Swinburne Astronomy Online Home Page

© Swinburne Copyright and disclaimer information
Maintained by: Rebecca Allen (rebeccaallen@swin.edu.au)
Authorised by: Prof. Jean Brodie (jbrodie@swin.edu.au)
Monday, 19-Nov-2007 11:19:37 AEDT