SAO Maths Primer
SAO Maths Primer |
|
Mathematics Primer: Derivatives
From a physical point of view the derivative is the rate of change of some physical quantity.
We will use speed to illustrate how the concept of derivative arises.
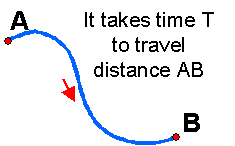
This is the average speed at which you travelled, but you might have have gone faster or slower in different parts of your trip from A to B. To know your speed in different parts of your trip you can divide the trip in smaller pieces, and then find your average speed for each of them.
But you might want to know your speed at a certain point (or moment) of your trip. The concept of
instantaneous velocity at one point arises naturally now. If the
pieces of your trip get smaller and smaller, you will be considering two points J and K closer and
closer to each other and it will take you shorter and shorter
Say you travel from A to B, and that it takes you some time T.
You know that your average velocity during your trip is:
Say that one of these small pieces of your trip consists of a section between two points J and K close to each other. Little amounts of some physical quantity (like distance here) are expressed in mathematics with the Greek letter 
, for example if s
is distance 
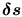means
a small distance. So in our case, we can say that from J to K you travelled a distance .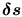
If you are at J and the time is s and it takes you a small time
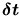to get to K, it
will be time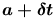 
when you are in K.
Then your average speed in your small-trip will be:
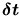times. So if you want to
know your speed at a certain moment you might consider the limit in which is going to zero
(this is when you are at point J):
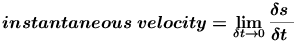
You will usually have a function describing the trajectory of the trip in terms of the time, say f(t). So,
and therefore the expression for the instantaneous velocity is:
The expression above is the rate of change of the distance with time or the derivative of the distance with respect to time.
At each point of the function where these limits exist, the function is said to have a derivative (or to be differentiable). The process of finding the derivative of a function is the fundamental operation of differential calculus.
Derivatives can also be considered from the geometrical point of view: the derivative is the slope of a curve (function) at a given point.
As an example we display the equation of mass conservation (which those of you studying the advanced SAO Unit HET611 Introduction to Stellar Astrophysics will find in Module 6 "Stellar Interiors", Activity 1 "What Holds a Star Up?".
 |
 |
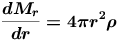This equation describes the rate of change of the star's mass M with distance r from the star's centre.
See also: limit, differential equations
Eric Weisstein's world of Mathematics mathworld.wolfram.com
S.O.S. Mathematics www.sosmath.com
Return to Maths Primer page
Back to the Swinburne Astronomy Online Home Page
©
Swinburne
Copyright and disclaimer information
Maintained by: Rebecca Allen
(rebeccaallen@swin.edu.au)
Authorised by: Prof. Jean Brodie (jbrodie@swin.edu.au)
Monday, 19-Nov-2007 11:19:37 AEDT