SAO Guest Contribution
SAO Guest Contribution |
|
Are the fundamental constants of nature really constant?
Tamara Davis
Tamara Davis is a PhD student working with Charles Lineweaver at the University of New South Wales in Sydney. Her research covers topics such as the nature of the expansion of the Universe, the nature of time and the meaning of Hubble's law beyond the particle horizon. In 2001 she joined with Paul Davies and in an extension of her previous work began to analyze the entropy of black holes as they cross the cosmological event horizon. Tamara was recently co-author of a paper that appeared in Nature entitled "Black holes constrain varying constants". She is a regular guest speaker for various astronomy and school groups and teaches a course for non-scientists on the scientific basis of the search for extra-terrestrial life.
Aside from physics Tamara also has an Arts degree in Philosophy, represents Australia in Ultimate frisbee and has received a University Blue for achievement in sport.
Recent observations suggest that the fundamental constants of nature may actually be varying. The jury is still out on whether the observations are correct but, if confirmed, the implications of such a discovery would be profound. Many of our cherished ideas, such as the constancy of the speed of light, may have to be rethought. This idea has been given worldwide media attention over the last few months. A paper written by Prof. Paul Davies, Dr Charles Lineweaver and myself, entitled "Black holes constrain varying constants" appeared in the 8th of August (2002) edition of Nature. To our great surprise it was at the centre of some of the recent interest. Our contribution was a small theoretical insight on how black hole thermodynamics might tell us which of the fundamental constants of nature is varying. The really interesting results come from the observations that showed the variation in the fine structure constant. In this guest presentation I'll try to clear up some misconceptions and give you glimpse into the most exciting aspects of this idea.
That the Universe is expanding is one of the fundamental tenants of modern cosmology. The leftover glow from the Big Bang, known as the cosmic microwave background (CMB), has been observed in great detail. It shows that the entire observable Universe was once at a common temperature. This poses a conundrum because large sections of our observable Universe have never been in causal contact - they have never been able to communicate because light moves too slowly to have crossed the distance between them. If they have never been in contact with each other, how do opposite sides of the observable Universe know what temperature to be?
In the early 1980's some physicists and astronomers came up with a possible solution to this problem (and several others). They proposed 'inflation', a period of exponentially accelerated expansion during the very early Universe before the CMB was emitted. Inflation means that the distant parts of our observable Universe were very close to each other before inflation occurred. Close enough that they were in causal contact and thermal equilibrium could be achieved. But what if there was another solution? What if everything was in causal contact because the speed of light was faster in the past?
This seemingly preposterous suggestion is exactly what was put forward by some astrophysicists in 1998. João Magueijo and Andy Albrecht, soon joined by John Barrow, Håvard Sandvick and several other researchers, pioneered a varying speed of light theory as a solution to some of these cosmological problems. A different varying-speed of light theory was presented independently by John Moffatt in 1993. However, prior to a 1998 paper by Webb et al., no measurement had ever given any indication that the fundamental constants could be varying. These varying speed of light theories, though interesting, were not widely recognised because they had no observational basis - they were just an (unlikely) alternative to inflation.
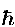, and the speed of light, c:
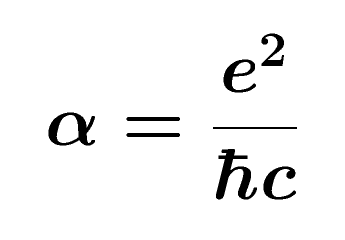
In rough terms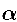 
is a measure of how tightly electrons are bound to protons in an atom and therefore effects the spectra of light they emit.
John Webb, Michael Murphy and collaborators have shown that the spectra from distant quasars are subtly different from the spectra given by measurements here on Earth. Moreover, the spectra differ in exactly the way we would expect if a change in the fine structure constant was responsible. Since the light emitted by these quasars has traveled billions of years to reach us, the evidence suggests that the fine structure constant was different in the past.
In slightly more detail, what they are observing is this: The light from distant quasars (some of the most energetic sources in the sky) travels to us through many billions of light years, and the space it travels through is not empty. Occasionally the light has to travel through slightly denser regions of gas and dust. As it travels past atoms and ions they absorb some of the light, but because atoms absorb only at specific wavelengths the light isn't absorbed evenly. Very precise dark lines appear in the spectrum where a particular atom absorbs, allowing us to identify the atom or ion doing the absorbing. Moreover each atom absorbs at more than one wavelength, so there are redundancy checks to make sure the correct absorber has been identified. The experimenters then compare the distant absorption spectra to laboratory measurements on Earth. The change they observe is so small (of the order 10-5 over the last 11 billion years), that it would be impossible to measure with a single observation. For that reason the group has observed 128 quasar absorption systems in many directions over the sky, and added up the effect from each different one. The analysis of this data indicates that the fine structure constant was smaller in the past. Statistically, it is a very strong result - the real question is whether there are unidentified systematic errors in the data.
Remarkable claims require remarkable evidence and none of the experimenters would currently claim that the evidence is conclusive. However, they have very carefully tried to avoid systematic errors that may be biasing the results. The method they use utilises many lines of the spectrum and a change in the fine structure constant shifts each line by different amounts and in different directions. Unlike a simple shift or stretching of the data, this complicated shift pattern is very difficult for a systematic error to mimic. Despite the apparent accuracy and integrity of the results, the investigators are not ruling out some as yet unnoticed systematic error. So far all of the observations have been made with just one instrument, the Keck 10m telescope on Mauna Kea in Hawaii, so it is impossible to completely rule out an aberration in the equipment. More measurements using different telescopes would reduce the possibility of error even further. Such observations are currently underway.
In the Davies, Davis and Lineweaver paper we assume the observations are correct and then ask 'which of the fundamental constants that make up 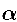is varying?' This is where black holes and thermodynamics can play a role. Thermodynamics is one of the most well established theories in science and it describes some of the most basics principles of our everyday life. The "Zeroth law of thermodynamics" states that when two bodies of unequal temperature are brought into contact, heat will flow from the hotter to the colder. The "First law of thermodynamics" states that energy is always conserved. The "Second law of thermodynamics" states that the total entropy in a system will always increase. It is the second law which we use to constrain varying constants.
Entropy is effectively a measure of disorder and is sometimes called the "arrow of time". A decrease in total entropy is as unexpected as time running backwards. The work of Jacob Bekenstein and Stephen Hawking in the 1970's showed that black holes aren't as black as they might seem. They radiate, they have a measurable temperature and they have entropy. The entropy of a non-spinning charged black hole is given by:
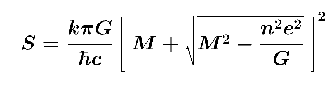
where the black hole has mass M and a charge of ne (n times the fundamental charge). Plank's constant is 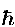, Boltzmann's constant is k and the gravitational constant is G.
The increase in the fine structure constant ,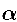
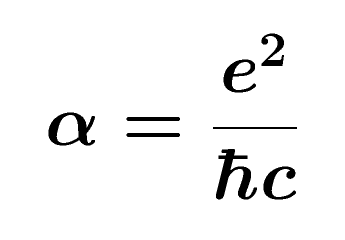
can be explained in two ways: (1) an increase in the value of e or (2) a decrease in the value of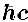 
. We can immediately see from the equation for the entropy of a black hole that these variations affect the value of black hole entropy in opposite ways. When 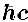decreases, entropy increases and the second law of thermodynamics holds. However, when e increases, entropy decreases and the second law of thermodynamics is violated. Thus black hole thermodynamics suggests that the increase in the fine structure constant is due to a decrease in Plank's constant or the speed of light.
The result stated above is tentative for several reasons. The main reason is that we have used the theories of general relativity and quantum mechanics to calculate the entropy of the black holes. Both these theories rely on the constancy of c, e and 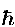. We assume that these theories are the "slow-variation" limit of a more fundamental varying-constant theory, in the same way that Newton's laws are the low-mass/low-velocity limit of general relativity. Nevertheless, it is quite possible for the varying-constant theories to have different solutions that don't agree with general relativity even in this slow-variation limit.
There are a variety of varying-constant theories, some involve varying speed of light, others varying charge. Observations do not yet distinguish between them. We have shown that black hole thermodynamics may provide a theoretical test for the theories. To be completely valid the black hole entropy needs to be calculated and tested in each theory separately. Unfortunately the solutions for black hole entropy in these theories are not yet known.
This section is a little technical but I mention it because it has caused considerable debate behind the scenes. Some claim that it is meaningless to ask which dimensional constant varies because only dimensionless constants are observable. To give a simple example take the speed of light; it is a dimensional constant because it is measured in metres per second. If we directly measure a decrease in the speed of light we have no way of knowing whether c really did decrease, or whether our metre rules all got longer (or our seconds shorter). We cannot distinguish whether the measured or the measurer changed.
That is why 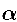, which is a number with no dimensions, is the constant obervers measure. Since 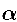has no units we can unambiguously tell when it changes.
But it gets worse: The confusion is not only between distance and metre sticks; a varying c in metres can actually be mimicked by a varying e in Coulombs. Given a single observation that indicates a varying c it is actually possible to choose to keep the speed of light constant and instead rescale the electric charge so it seems like e is changing. Complicated! Barrow & Magueijo (1998) show how a varying speed of light cosmology, through changes of standard units, can be rephrased as a varying e theory. The question is then 'does it matter which constant we say is varying if we can create a mirror theory with a different varying constant that predicts the same observations?'
It does matter because the different theories of varying constants predict very different, and testable, observations. A change in the speed of light affects causality and may therefore be able to replace inflation in the very early Universe. On the other hand, a change in the electric charge affects how molecules and atoms hold together; if it changed dramatically then carbon wouldn't hold together and life as we know it would cease to exist. The predictions of these models don't change if we use some mathematical gymnastics to make it look like the other constant is varying. When the varying speed of light theory suggested by Magueijo is recast as a varying electric charge theory it does not become the varying e theory proposed by Bekenstein. When it becomes a varying e theory it still predicts the same observables as the simple varying c theory it started as - the difference is that the dynamics in the new theory are very complicated.
Moreover, when an independent dimensionless constant is introduced, for example the dimensionless mass of the electron:
 |
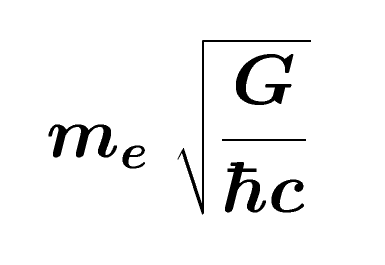, that includes Newton's gravitational constant G, this duality between e and c can be broken. |
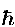. This technicality is completely avoided if you calculate black hole entropy from within a varying-constants theory. The theories restrict what is constant and what varies so there is no ambiguity. We can then check whether the theory matches observations and passes theoretical criteria such as the black hole thermodynamics test.
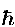is responsible for the change is interesting because the different varying-constant theories predict different observational results and could solve some of the mysteries of the early Universe. Black hole thermodynamics suggests that c or 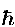should be preferred over e as the constant responsible for the variation. As long as black hole entropy remains uncalculated in varying-constant theories, this result remains far from conclusive. This is research-in-progress and the next couple of years should uncover some interesting results. Watch this space...