Cosmos


COSMOS - The SAO Encyclopedia of Astronomy › S

Semi-major Axis

semi-majoraxis.jpg
An ellipse with semi-major axis, a.

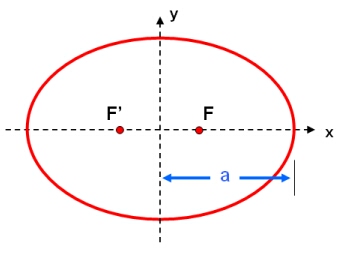
The semi-major axis, a, is half of the longest diameter of an ellipse. Together with the semi-minor axis , b, and eccentricity, e, it forms a set of related values that completely describe the shape of an ellipse:

b2 = a2(1-e2)

In cartesian coordinates (x,y), an ellipse is the solution of:

$ \left(\frac xa\right)^2 + \left(\frac yb\right)^2 = 1 $

or in polar coordinates (r,θ):

$ r = \frac{a(1-e^2)}{1+e\cos\theta} $


Study Astronomy Online at Swinburne University
All material is © Swinburne University of Technology except where indicated.