Semi-major Axis
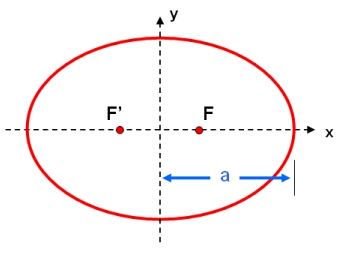
The semi-major axis, a, is half of the longest diameter of an ellipse. Together with the semi-minor axis , b, and eccentricity, e, it forms a set of related values that completely describe the shape of an ellipse:
b2 = a2(1-e2)
In cartesian coordinates (x,y), an ellipse is the solution of:
![]()
or in polar coordinates (r,θ):
![]()
Study Astronomy Online at Swinburne University
All material is © Swinburne University of Technology except where indicated.

