Summation | COSMOS

The addition of a sequence of numbers can be represented with the summation symbol (Σ).

Consider an addition sequence, S_n. Suppose the numbers to be added are u₁, u₂, u₃, …, u_n. We let

$\begin{align*} S1 &= u1\\ S2 &= u1 + u_2\\ S3 &= u1 + u_2 + u_3\\ &\ldots\\ Sn &= u1 + u2 + \ldots + un = \sum\limits_{k=1}^n u_k \end{align*}$

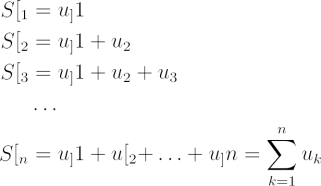The sigma (Σ) symbol represents a summation of n components. As n increases without bound…

$u_1 + u_2 + \ldots + u_n + \ldots$

…we are led to consider a summation over infinite components, which is denoted by

$\sum\limits_{k=1}^{\infty} u_k$

Such an expression is called an infinite series. As an example, we can write the equation of state for a mixture of gases:

$P = \sum\limits_i P_i = \sum\limits_i n_ikT$	where P = total pressure
		P_i = partial pressures of all i gas species
		n_i = particle number per unit volume
		k = Boltzmann’s constant, and
		T = temperature

This equation describes the total pressure P, as the summation of partial pressures P_i.