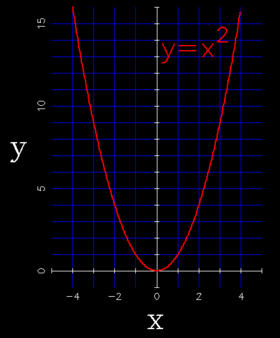
In astronomy, the parabola features in both the construction of telescopes and in the motion of comets around the Sun. A parabola is one of the four conic sections – a plane intersecting a cone parallel to one edge traces out a parabola.	The most basic parabola y = x2 Credit: Swinburne
A parabola has the functional form:
y = A x2
where A is the constant of proportionality.

Parabolas in Telescope Design

Demonstration of how a parabola focuses light from a plane wave source. For this reason many telescopes such as the Parkes and Lovell antennae use parabolic surfaces to reflect light to a point where a detector or receiver is placed. Credit: Swinburne

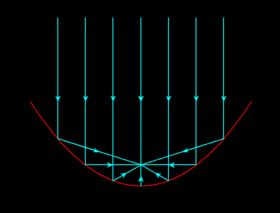
The parabola is the exact shape required to focus a plane wave to a single point. Hence parabolic dishes coherently (i.e. in phase) add electromagnetic radiation at a point and are central to many telescope designs in both the optical and radio. For a parabola of equation y = A x2, the point of focus lies at ( x = 0, y = A/4).

Parabolas in Nature

Curiously a comet falling from a great distance towards the Sun will trace out a parabolic orbit with the Sun at the focus of the parabola. This is just a consequence of Newton’s laws of motion and gravitation. Similarly a projectile on Earth follows a parabolic arc as it falls under gravity.