Gaussian Function
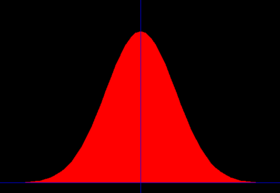
A Gaussian function, or distribution, has the form:
![]()
where σ is the standard deviation, and μ is the x-offset of the Gaussian function from zero.
Gaussian functions approximate the shapes of many observables in astronomy, such as the profiles of seeing disks, the width of spectral lines, and the distribution of noise in radio receivers.
In error analysis, the Gaussian function is often used to determine the significance of a measurement, as the distribution function of a random set of measurements in the presence of noise is well approximated by a Gaussian function. Astronomers like to talk about whether a result is 2-σ, or 3-σ etc. This refers to the likelihood that an experimental result is a certain number of standard deviations from the measured value. 67% of all results are within 1-σ of the mean whereas 95.4% of within 2-σ and 99.7% with 3-σ. Thus a 1-σ result is 33% likely to be due to random fluctuations, whereas a 3-σ result is very secure.
The Gaussian distribution is sometimes called the “normal distribution”.
Study Astronomy Online at Swinburne University
All material is © Swinburne University of Technology except where indicated.

