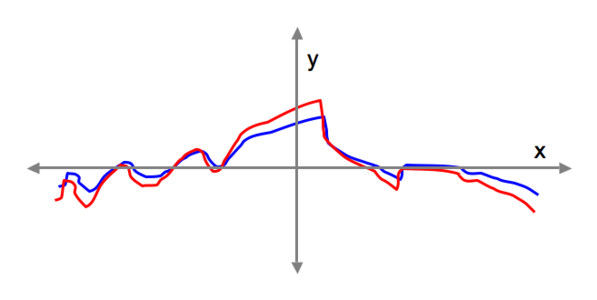
Two functions are said to be correlated when the sum of the product of their elements are positive.

The red and blue functions shown here are highly correlated.
Credit: Swinburne University of Technology

The correlation coefficient c of two finite sets of numbers x_i, y_i is defined as:

If the correlation coefficient is 1, the sets are said to be 100% or perfectly correlated - in this case the two functions are linearly proportional to each other. On the other hand if the correlation coefficient is -1, the sets are anti-correlated.

Data which are highly correlated have coefficients near unity and look very similar to the eye sharing the same shape.

Two digital streams of data can have their correlation coefficient calculated as a function of time lag, which is called the cross correlation function.

In radio astronomy, the fourier transform of the cross correlation function allows the power spectrum to be computed, thus enabling spectroscopic studies of atomic and molecular emission and absorption lines.