Constructive Interference
A pair of light or sound waves will experience interference when they pass through each other. The individual waves will add together (superposition) so that a new wavefront is created.
Constructive interference occurs when the maxima of two waves add together (the two waves are in phase), so that the amplitude of the resulting wave is equal to the sum of the individual amplitudes. Equivalently, the minima of the waves would be aligned.
The images below show the effects of constructive interference between two waves with the same amplitude and frequency (ω) described by the equations:
![]() and
and ![]()
where δ is the phase difference between the waves, k is the wave number, x is the wave position and t is time.
|
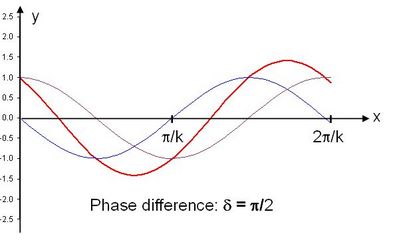
In the image on the left, the phase difference is δ = π/2 or 90 degrees. The two waves (thin lines, shown in blue and purple) interfere, with the resulting wave (shown in red) equal to the sum of these two waves. Note that the nodes of the two original waves (where the waves cross the y=0 axis) do not occur at the same values of x, and the nodes of the resulting wave occur when y1 + y2 = 0. |
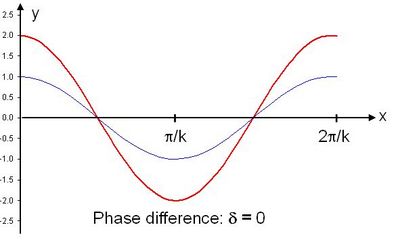
| In the image on the right, the phase difference is δ = 0, so that the two waves (shown in blue) interfere constructively and the amplitude of the resulting wave (shown in red) is the sum of the individual amplitudes. The nodes of the final wave occur at the same locations as the nodes of the individual waves. |
|
For interference of light waves, such as in Young’s two-slit experiment, bands of bright and dark lines will appear. The bright regions occur whenever an integer number of waves constructively interfere.
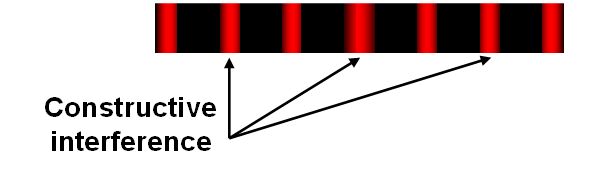
The alternative to constructive interference is destructive interference, when the waves are 180 degrees out of phase.
Study Astronomy Online at Swinburne University
All material is © Swinburne University of Technology except where indicated.

