Angular Velocity

For rotational motion about a point or axis, angular velocity is the rate of change of the angular position with time, or in other words the derivative of the angular position with time:

$\omega = \frac{d\theta}{dt}$ = angular velocity,	where	θ = the angular position
$\omega = \frac{d\theta}{dt}$ = angular velocity,		t = time

The direction of the angular velocity vector is perpendicular to the plane of rotation as given by the right-hand rule. The angular velocity is expressed in units of [angular distance/time], often radians per second.

For an object moving in a curved path it can be useful to describe the motion using both angular and linear velocities. Using a fundamental relation for circular geometry:

		$\theta = \frac{s}{r}$
	where	θ = angle
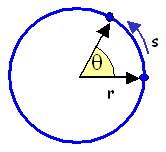
		s = arc subtended by θ
		r = radius of the circle

The magnitudes of the linear and angular velocities are related by:

$v = \frac{ds}{dt} , \omega = \frac{d\theta}{dt} \rightarrow v = r\omega$	where	v = linear velocity
			r = distance from the axis of rotation
		ω = angular velocity

Note that we are not using vector notation in this expression, rather it is the magnitude of the velocities that follow the relation.

A	B	C	D	E
F	G	H	I	J
K	L	M	N	O
P	Q	R	S	T
U	V	W	X	Y
Z	All