Cosmos


COSMOS - The SAO Encyclopedia of Astronomy › T

Time Average

The time average of a function is found by evaluating the integral:

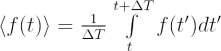
$ \left\langle f(t)\right\rangle = \frac1{\Delta T}\int\limits_t^{t+\Delta T}f(t^\prime)dt^\prime $

with the average taken over a time, ΔT.

Time averages are often important when considering oscillating waves of the form:

$ f(t) = A\sin(\omega t) $

where ω is the angular frequency and A is the amplitude. The instantaneous value of this wave varies between -A and A, however, the time average of this wave over one period is $ \langle f(t)\rangle = 0 $.

Another common example (such is in the calculation of the intensity of an electromagnetic wave) is to find the time average of the functions

$ f(t) = \sin^2(\omega t) $
and $ g(t) = \cos^2(\omega t) $

Using the equation (1) above, it can be shown that:

$ \langle f(t) \rangle = \langle g(t) \rangle = \frac 12 $.


Study Astronomy Online at Swinburne University
All material is © Swinburne University of Technology except where indicated.