For rotational motion about a point or axis, angular velocity is the rate of change of the angular position with time, or in other words the derivative of the angular position with time:

= angular velocity,	where	θ = the angular position
		t = time

The direction of the angular velocity vector is perpendicular to the plane of rotation as given by the right-hand rule. The angular velocity is expressed in units of [angular distance/time], often radians per second.

For an object moving in a curved path it can be useful to describe the motion using both angular and linear velocities. Using a fundamental relation for circular geometry:

	where	θ = angle
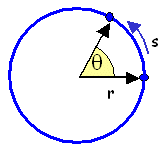
		s = arc subtended by θ
		r = radius of the circle

The magnitudes of the linear and angular velocities are related by:

	where	v = linear velocity
		r = distance from the axis of rotation
		ω = angular velocity

Note that we are not using vector notation in this expression, rather it is the magnitude of the velocities that follow the relation.