SAO Maths Primer

An example of a logarithm is as follows. In the expression above, if the base b is equal to 10 and N is a number equal to 100, then x is equal to 2 and is said to be the logarithm of 100 to the base 10.
This is written: log 100 = 2, in which it is understood that log means logarithm to the base 10. Logarithms to the base 10 are also called a common logarithm.

Logarithms that employ the base e, in which e = 2.71828 ... are called natural, or Napierian logarithms; the notation used is ln, to distinguish natural logarithms from common logarithms (log).

As an example of an expression used in astronomy that includes logarithms, we display the equation for the Distance Modulus of an object (i.e. the difference between the apparent and absolute magnitude of the object, which is a measure of the distance to the object)

So why do you think we want to use logarithmic scales?

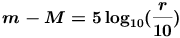Why would anyone want to use a logarithmic method? Let's consider an astronomer, who wants to illustrate the amount of money he/she owned (or hopes to own) at particular ages of his/her life.

The problem is, that when we draw a graph of Money versus Age, the detail near the beginning isn't clear. This is because the vertical scale has to go up to $100,000, so amounts like $1, $5 and $10 are too tiny to show.

The solution is to draw the graphic again but this time using a logarithmic vertical scale, where you increment the y-axis by factors of ten (i.e. axis units are 10, 100, 1,000 ...) This is just like expressing the vertical scale as the logarithm in base 10 of the money owned (i.e. y = log(Money)). Any scale that increases by multiplying rather than by adding is called a logarithmic scale.

Using logarithmic scales is particularly useful when drawing graphs in astronomy, when amounts that need to be plotted can greatly vary in size.

For example, this graphic shows the luminosity-period relation for 1500 variable stars in the Large Magellanic Cloud. As you can see the horizontal axis gives the period (P) using a logarithmic scale. If you didn't draw it this way you wouldn't be able to appreciate variations for small values of P, just like in our example above you couldn't see the difference between amounts like $1, $5 and $10.

Recommended Web Sites:

Eric Weisstein's world of Mathematics mathworld.wolfram.com

S.O.S. Mathematics www.sosmath.com

Return to Maths Primer page