Mathematics Primer for HET611 Introduction to Stellar Astrophysics

Students in HET611 Introduction to Stellar Astrophysics will be exposed to detailed mathematical concepts and equations. We assume introductory, tertiary (post-secondary) level mathematics & physics.

The following is a "primer" for students and will discuss some important mathematical terms and quantities used in HET611. We strongly recommend that you familiarise yourself with the primer and if need be, use the recommended links to more information regarding mathematics.

This primer contains information on

• The Logarithmic Scale
• Limits
• Derivatives and Integrals
• Differential equations

The Logarithmic Scale:

Logarithm is the exponent or power to which a base (number) must be raised to yield a given number.

An example of a logarithm is as follows. In the expression b^x = N, if b is the base and equal to 10 and N a number, equal to 100, then x is equal to 2 and is said to be the logarithm of 100 to the base 10.

This is written: log 100 = 2, in which it is understood that log means logarithm to the base 10. The latter is also called a common logarithm. Logarithms that employ the base e, in which e = 2.71828 ... are called natural, or Napierian, logarithms; the notation used is ln, to distinguish natural logarithms from common logarithms (log).

When a common logarithm of a number is written as the sum of an integer and a positive decimal (e.g., 2.3147), the integer--called the characteristic--serves to locate the decimal point in the number, and the decimal--called the mantissa--indicates the digits in the number. The latter are determined from tables of logarithms, which relate mantissas to numbers. When the number is greater than or equal to 1, the characteristic is 1 less than the number of digits to the left of the decimal point; when the number is less than 1, the characteristic is negative and is 1 more than the number of zeros following the decimal point. For example, the number 365.0 has the characteristic 2; the number 0.005 has the characteristic -3.

As an example from HET611, we display the equation that describes the Distance Modulus of an object from Module 3 "Physical Parameters", Activity 1 "How Bright is a Star?". This equation describes the Distance Modulus, m-M, as the logarithm (to the base 10) of the distance to an object (in this case, r/10) all multiplied by 5.

Limits:

The limit of a function is simply what value the function approaches as we approach (very closely) a specific input value. Limits can be thought of as describing the very small scale behaviour of a function.

So, let us consider a function, f(x). The limit is concerned with what f(x) looks like around the point x = a. The formal statement says that the limit L is the number such that if you take numbers arbitrarily close to a that the result of f applied to those numbers must be arbitrarily close to L.

The formal definition is given by the following statement: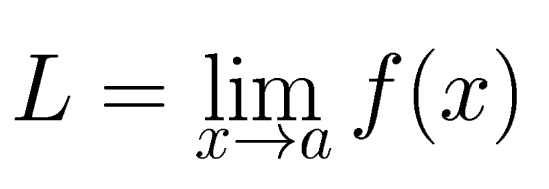

We shall use the property of limits in defining the instantaneous velocity in the section on Derivatives, below.

Derivatives and Integrals:

Derivatives:

From a physical point of view: the derivative is the rate of change of some physical quantity.

We will use speed to illustrate how the concept of derivative arises.

Say you travel from A to B, and that it takes you some time T. You know that your average velocity during your trip is:

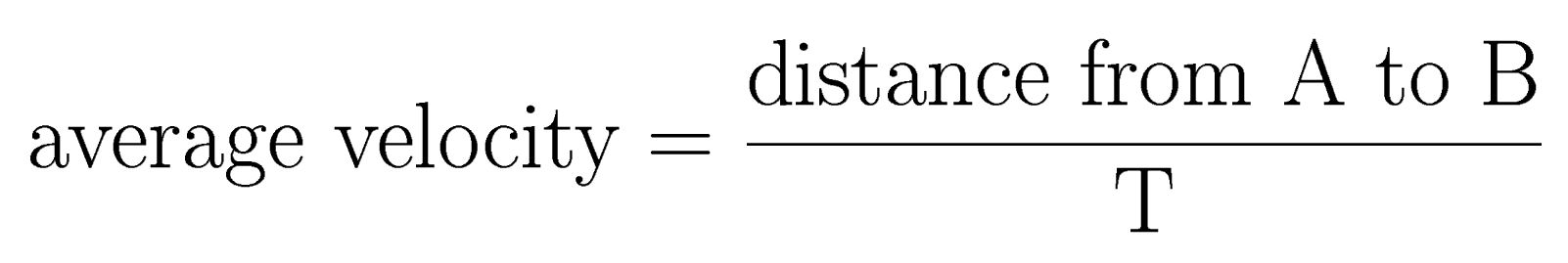
This is the average speed at which you travelled, but you might have have gone faster or slower in different parts of your trip from A to B. To know your speed in different parts of your trip you can divide the trip in smaller pieces and then find your average speed for each of them.
Say that one of this small pieces of your trip consists of a section between two points J and K close to each other. Little amounts of some physical quantity (like distance here) are expressed in mathematics with the Greek letter  , for example if s is distance  s means a small distance. So in our case, we can say that from J to K you travelled a distance  s.
If you are at J and the time is a and it takes you a small time  t to get to K, it will be time a +  t when you are in K.
Then your average speed in your small-trip will be:

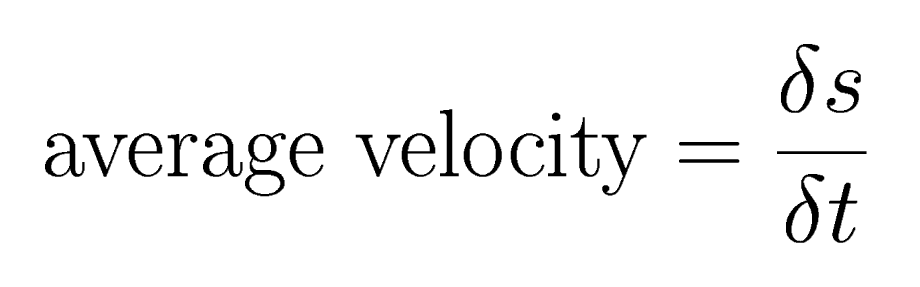
But you might want to know your speed at a certain point (or moment) of your trip. The concept of instantaneous velocity at one point arises naturally now. If the pieces of your trip get smaller and smaller, you will be considering two points J and K closer and closer to each other and it will take you shorter and shorter  t times. So if you want to know your speed at a certain moment you might consider the limit in which   is going to zero (this is when you are at point J):

You will usually have a function, f, describing the trajectory of the trip in terms of the time, say f(t). So at time a you are at f(a) and after a time  t you are at f(a+ t). Then the distance you have travelled is f(a+  t)-f(a) and therefore the expression for the instantaneous velocity is:

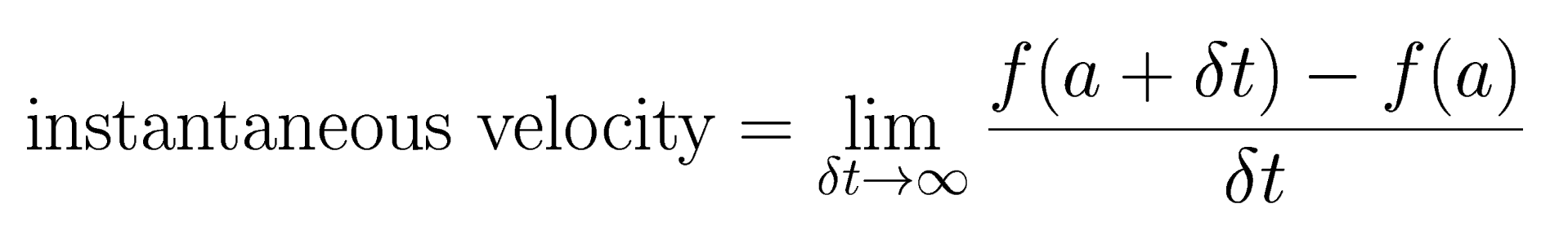
The above expression is the rate of change of the distance with time or the derivative of the distance with respect to time.

At each point of the function where these limits exist, the function is said to have a derivative (or to be differentiable. The process of finding the derivative of a function is the fundamental operation of differential calculus.

(Derivatives can also be considered from the geometrical (mathematical) point of view: the derivative is the slope of a curve (function) at a given point.)

As an example from HET611, we display the equation of mass conservation from Module 6 "Stellar Interiors", Activity 1 "What Holds a Star Up?". 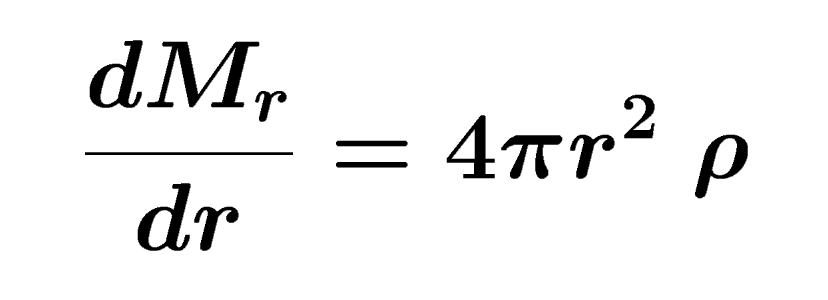This equation describes the rate of change of the mass, M with distance, r from the stars centre.

Integrals:

Let us now discuss integrals or integral calculus, the other main branch of differential calculus. Usually, "to integrate" has two meanings. Firstly, it has a non-technical definition, "to indicate the whole of; to give the sum or total of" (Webster). Mathematically, this meaning is represented by finding areas bounded by curves, volumes of solids, lengths of curves, etc. An integral is a mathematical object which can be interpreted as an area or a generalization of area.

Another mathematical meaning of "to integrate" is "to find a function whose derivative is given". Other words for integral include antiderivative or inverse derivative. Formally, a function, y=F(x) is a called a solution of the differential equation

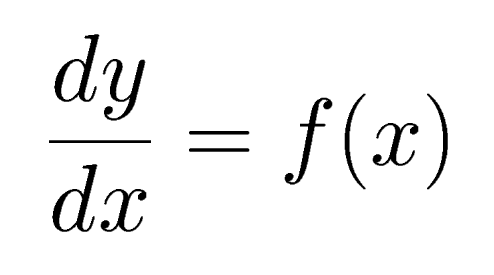
... if over the range a < x < b, F(x) is differentiable and

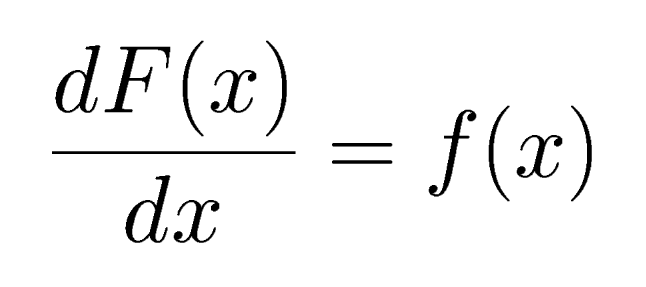
We can also say that in these circumstances, F(x) is an integral of f(x) with respect to x.

Further, if y=F(x) is any solution then all solutions are contained in the formula

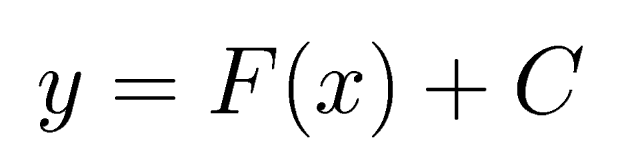
where C is an arbitary constant. This is indicated by the following

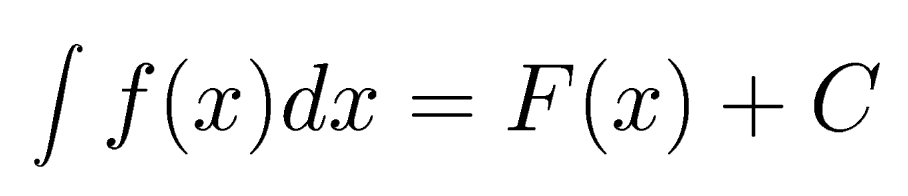
... where the symbol

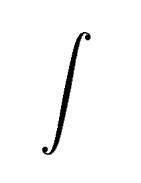
is called an "integral sign" and the previous equation is read "The integral of f(x)dx is F(x) plus C". We may interpret this by thinking of the symbol

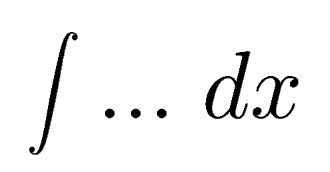
as meaning "integral, with respect to x, of ...". This symbol may then be interpreted as the inverse of the symbol

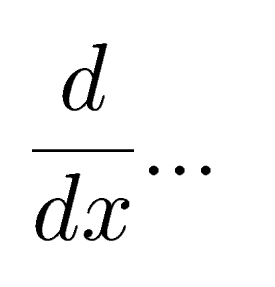
As an example from HET611, we display an equation describing total luminosity from Module 3 "Physical Parameters", Activity 1 "How Bright is a Star?". 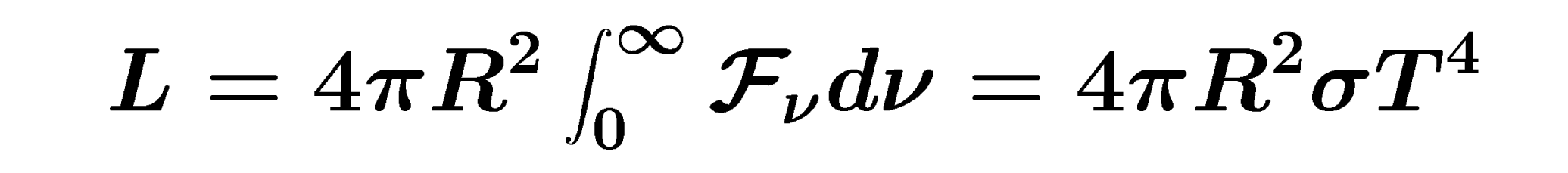This equation describes the luminosity of a star with radius R, with flux emitted at the stars surface, Fnu. There are limits in frequency given, 0 and infinity, over which the flux is integrated (ie. summed), to give total flux.

Differential Equations:

A differential equation is an equation that consists of an unknown function and its derivatives.

Suppose a quantity changes at a rate that at any instant of time t is proportional to the amount x present at that instant. This can be expressed by the differential equation:

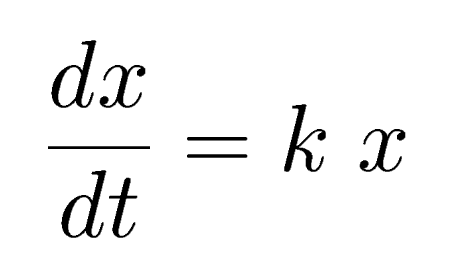
where k is a proportionality constant. If the amount present at time t=0 is x₀ the initial condition x=x₀ when t=0 eneables us to evaluate the constant k.

As an example from HET611, we display the equation of radiative transport from Module 6 "Stellar Interiors", Activity 2 "Energy Transport". 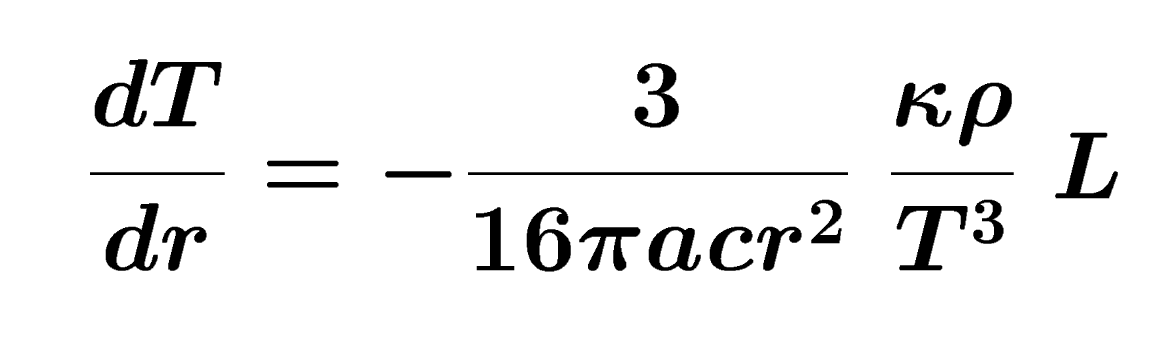This equation shows that the rate of change of temperature with radius is related to several constants, opacity, density, luminosity and (inversely) to the cube of the temperature itself.

Recommended Web Sites:

Eric Weisstein's world of Mathematics mathworld.wolfram.com

S.O.S. Mathematics www.sosmath.com