Schwarzschild Lens
The Schwarzschild lens model is the simplest gravitational lens model. It treats the lensing object as a point mass in the lens plane, and always produces two images (although one image may be highly demagnified).
For the Schwarzschild lens, the deflection angle, ![]() , is:
, is:
![]()
where M is the lens mass, ![]() is the impact parameter in the lens plane, G is the gravitational constant and c is the speed of light. The closer a light ray passes to the lens, the greater the deflection.
is the impact parameter in the lens plane, G is the gravitational constant and c is the speed of light. The closer a light ray passes to the lens, the greater the deflection.
If we use the dimensionless gravitational lens equation:
y = x – α(x)
relating positions in the source plane, y and lens plane x, the deflection angle for the Schwarzschild lens reduces to:
α(x) = 1/x
This equation can be inverted to give a simple quadratic equation, and hence ![]() (the two image locations) as a function of y. We now have enough information to determine:
(the two image locations) as a function of y. We now have enough information to determine:
- The location of the source, if we know the location of one or both of the images, using y = x – 1/x; and
- The location of both images, if we know the location of the source, using
![$ x_\pm = \frac12\left[y\pm \sqrt{y^2+4}\right] $](/cosmos/files/tex/b4b8aeca45f0237f558e8e8be2d22ef50216294a.png) . The corresponding gravitational magnifications of the two images are
. The corresponding gravitational magnifications of the two images are 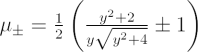 .
.
For a point source which is directly in line with the observer and a Schwarzschild lens, the image will be a ring with radius:
![]()
called the Einstein ring or Einstein radius. The distances, Dij, are angular diameter distances between the [O]bserver, [L]ens and [S]ource planes.
Study Astronomy Online at Swinburne University
All material is © Swinburne University of Technology except where indicated.

